How Linear Algebra Is Used In Machine Learning

Linear Algebra for Machine Learning: An Introduction

If yous've started looking into backside the scenes of popular machine learning algorithms, you might take come up across the term "linear algebra".

The term seems scary, but it isn't actually so. Many of the machine learning algorithms rely on linear algebra considering it provides the ability to "vectorize" them, making them computationally fast and efficient.

Linear algebra is a vast branch of Mathematics, and not all of its noesis is required in understanding and edifice machine learning algorithms, so our focus will exist on the bones topics related to car learning.

This article covers the fundamentals of linear algebra required for machine learning, including:

Vectors and Matrices
Matrix Operations (Multiplication, Addition, and Subtraction)
Vector Operations (Addition, Subtraction, and Dot Product)

NumPy implementations for each of the operations are also included at the end of each topic.

Matrices

A matrix is a rectangular assortment of numbers bundled in rows and columns. In other words, a matrix is a ii-dimensional assortment comprising of numbers.

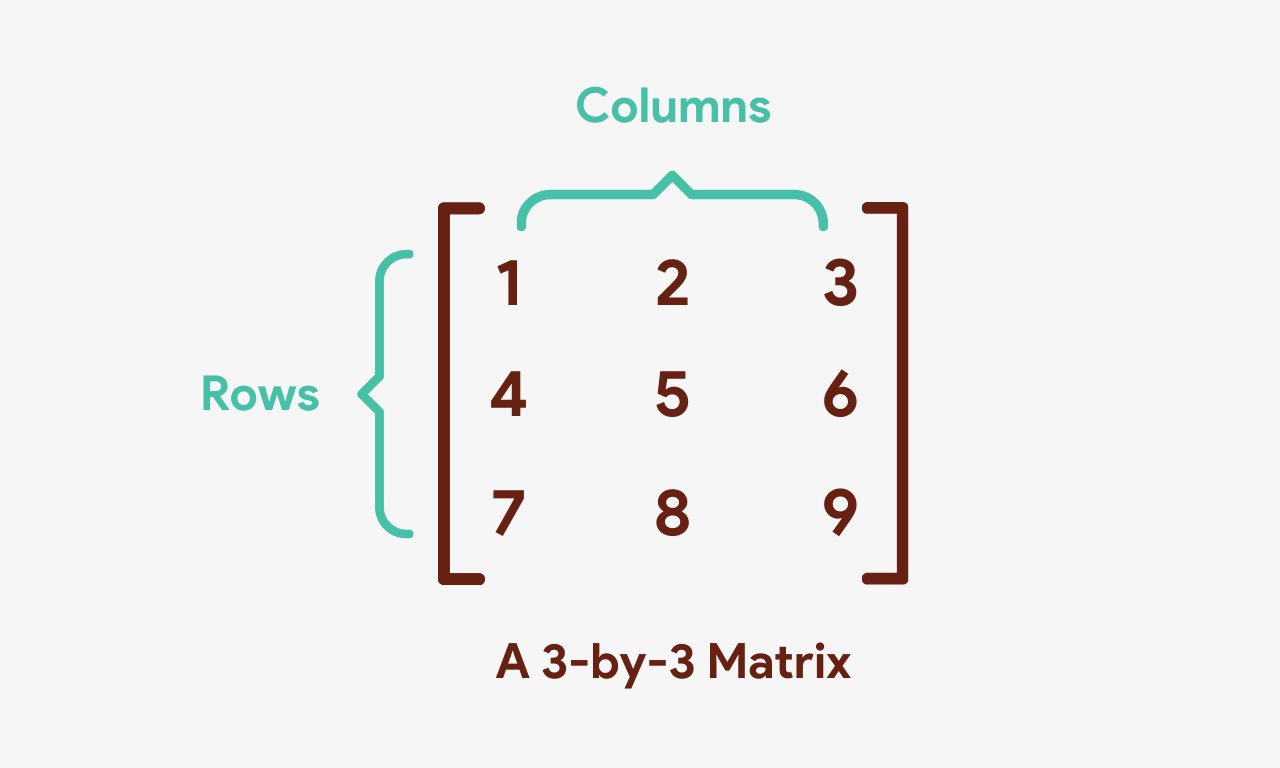
The dimensions of a matrix are denoted by g ✕ n , where m is the number of rows and n is the number of columns it has. The matrix shown in the above paradigm is a three ✕ 3 matrix since it has 3 rows and 3 columns.

Python, by default, doesn't come up with arrays. Lists are bully, but they aren't very efficient when performing millions of numeric options. To solve this problem, we use some sort of numerical computing library, which supports arrays and fast numeric computations. NumPy is one of them and it has several other benefits autonomously from that.

This is how we can create a 3x3 matrix using NumPy:

Row and Cavalcade Matrices

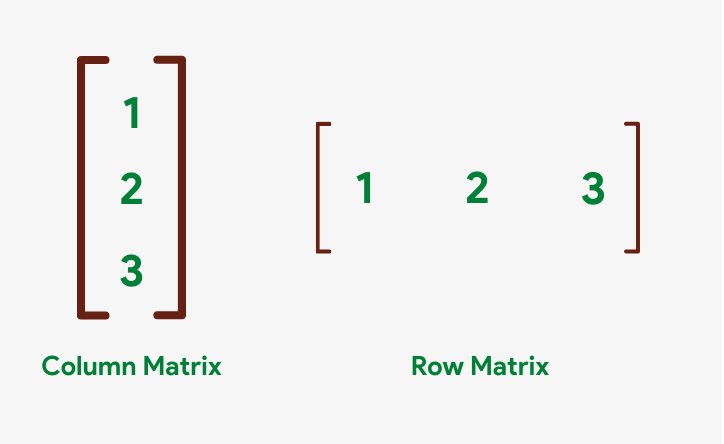
Based on the arrangement of rows and columns, matrices are divided into several types. Two of them are row and column matrices.

A matrix having only i cavalcade is called a column matrix while a matrix having only one row is chosen a row matrix.

Operations on Matrices

Matrices support all of the basic arithmetics operations, including addition, subtraction, multiplication, and partition.

Addition

Adding two matrices is very simple. The corresponding elements of the matrices are added together to form a new matrix. The resulting matrix also has the aforementioned number of rows and columns as the two matrices to exist added.

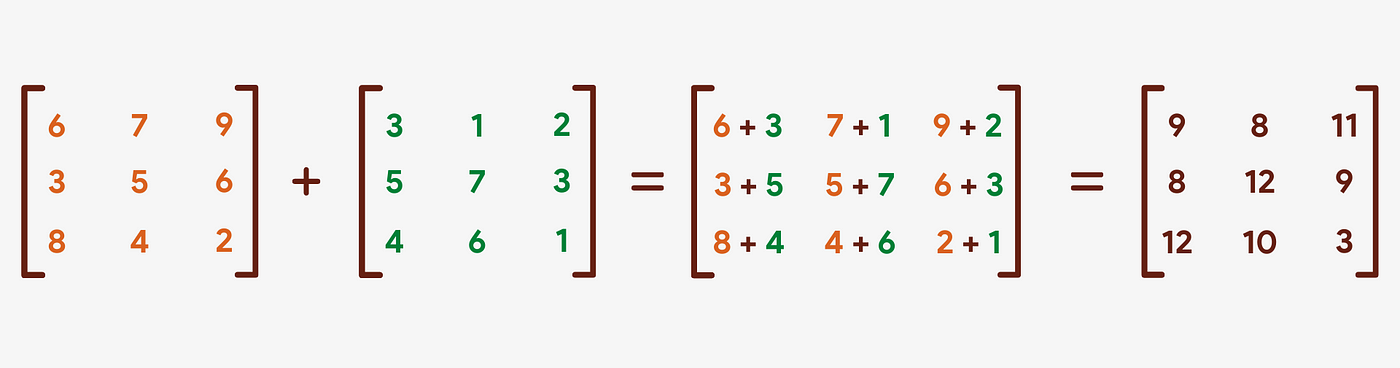
Note that both of the matrices should accept the same number of rows and columns, otherwise the result volition exist undefined.

Subtraction

Subtracting two matrices is merely as uncomplicated as the improver. The corresponding terms of the two matrices are subtracted to form a new result matrix. Just like in add-on, both of the matrices should have the same dimensions.

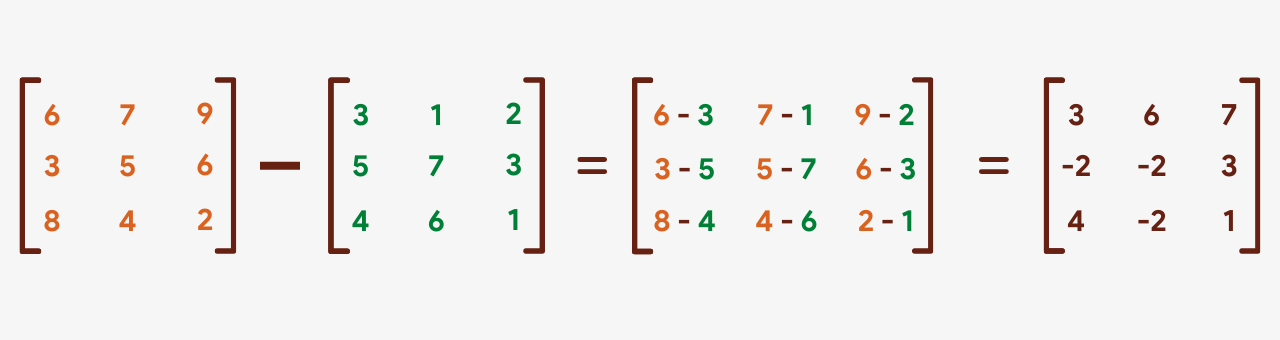
Scalar Multiplication

Multiplying a matrix by a number is called scalar multiplication. This kind of multiplication is very like shooting fish in a barrel, as we simply take to multiply each of the elements of the matrix by that number.

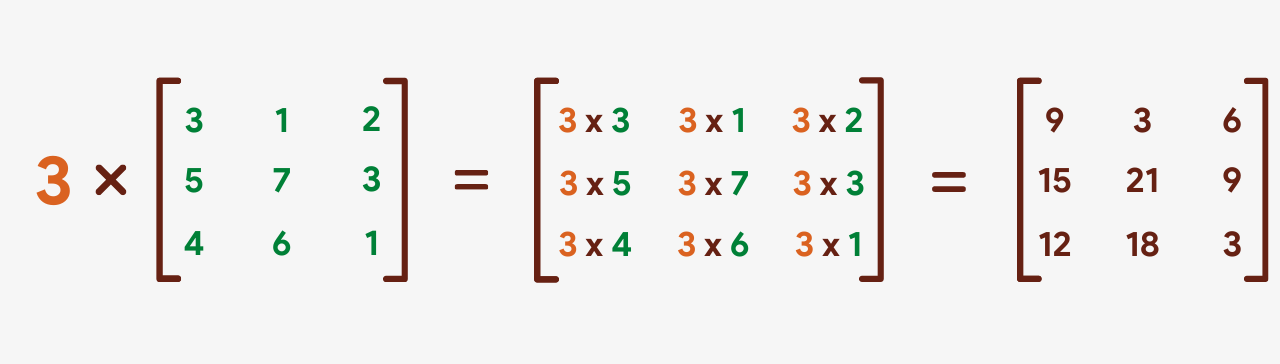
Scalar Division

Dividing a matrix by a scalar is as well very simple. Each of the elements in the matrix is divided by the number to form a new upshot matrix.

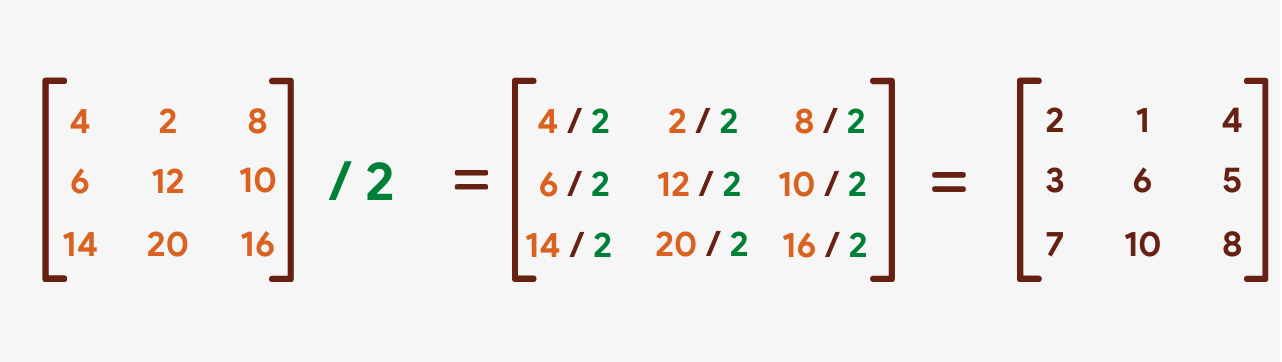
Matrix-Matrix Multiplication

Multiplying a matrix by another matrix is called "matrix multiplication" or "cross product". Matrix multiplication is very piece of cake, just a fleck tricky for beginners to understand.

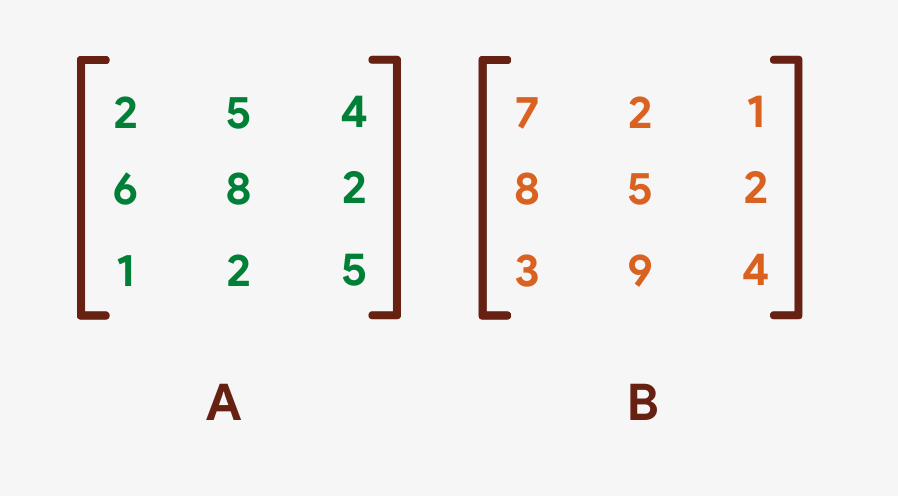
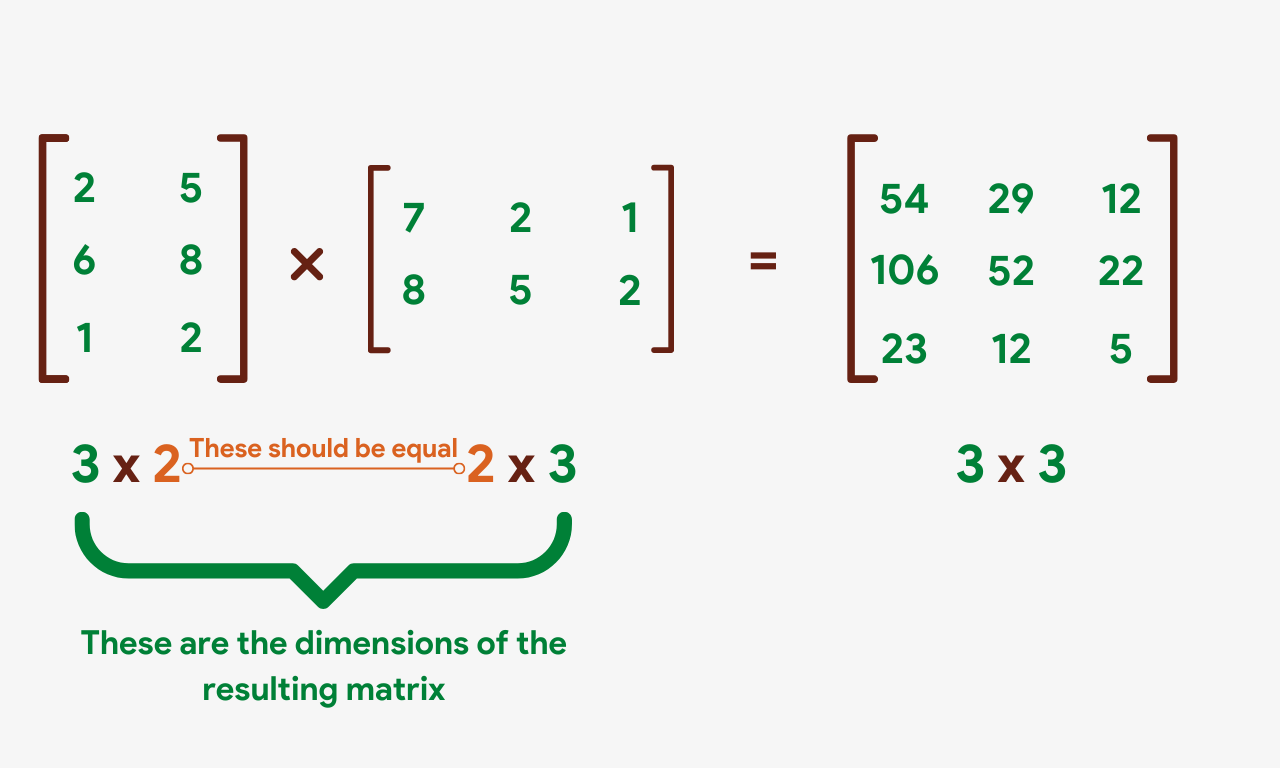
Let'southward accept 2 threex3 matrices, A and B, as shown beneath:

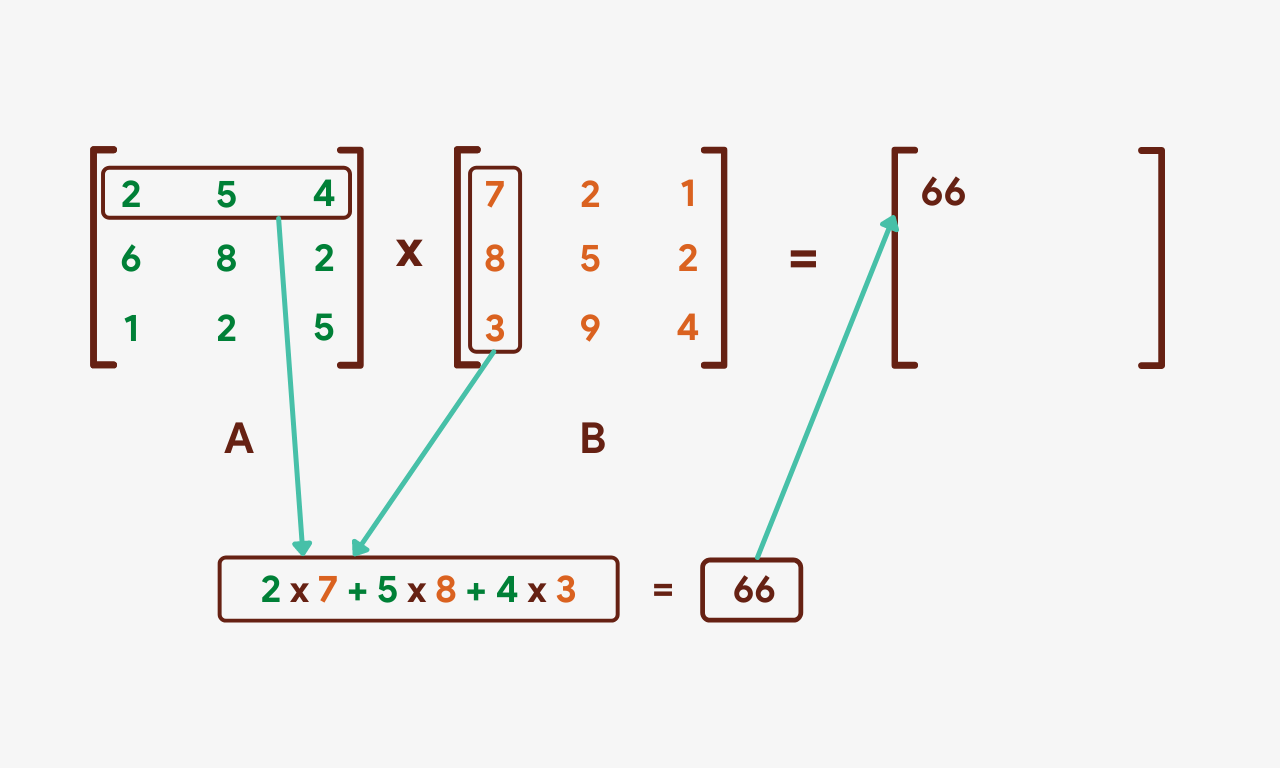
To begin with, nosotros'll multiply each of the numbers in the first row of A by the corresponding numbers in the first cavalcade of B. The sum will and then be put in the result matrix as shown beneath:

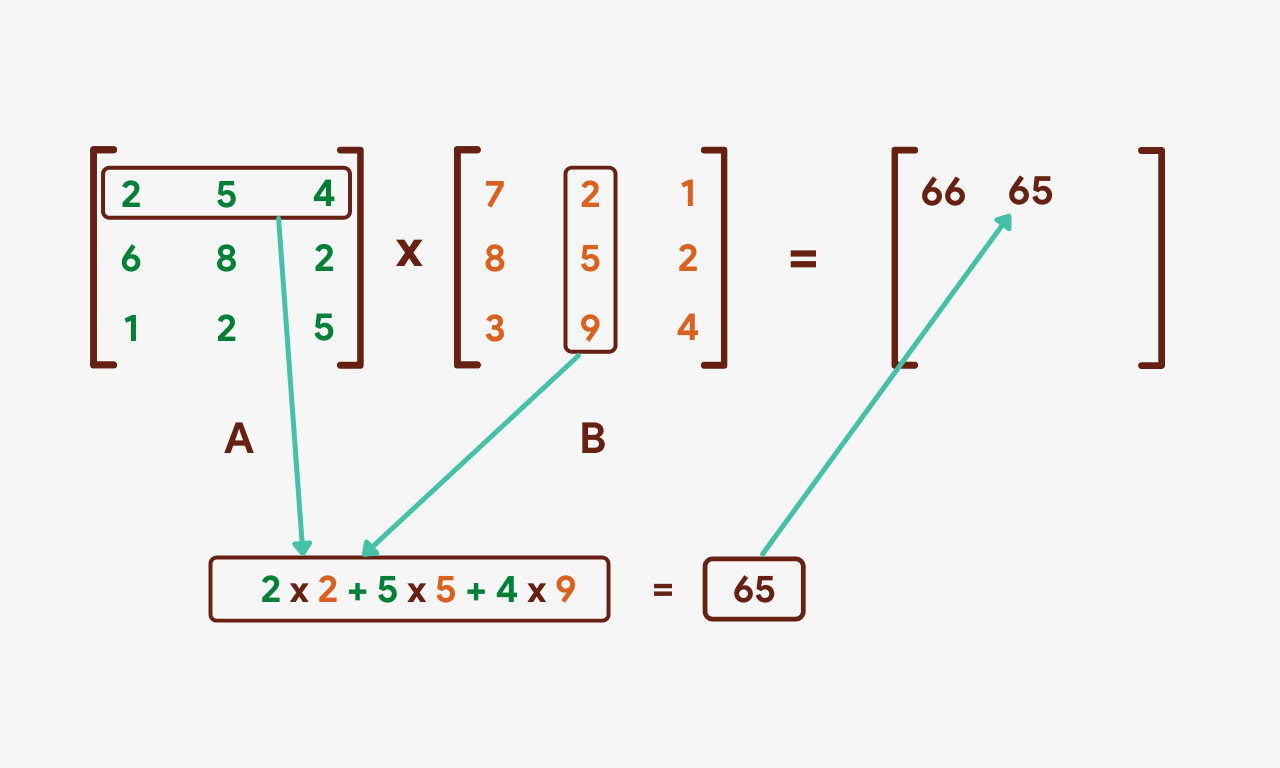
We'll over again take the product of the kickoff row of matrix A but this time with the second cavalcade of matrix B.

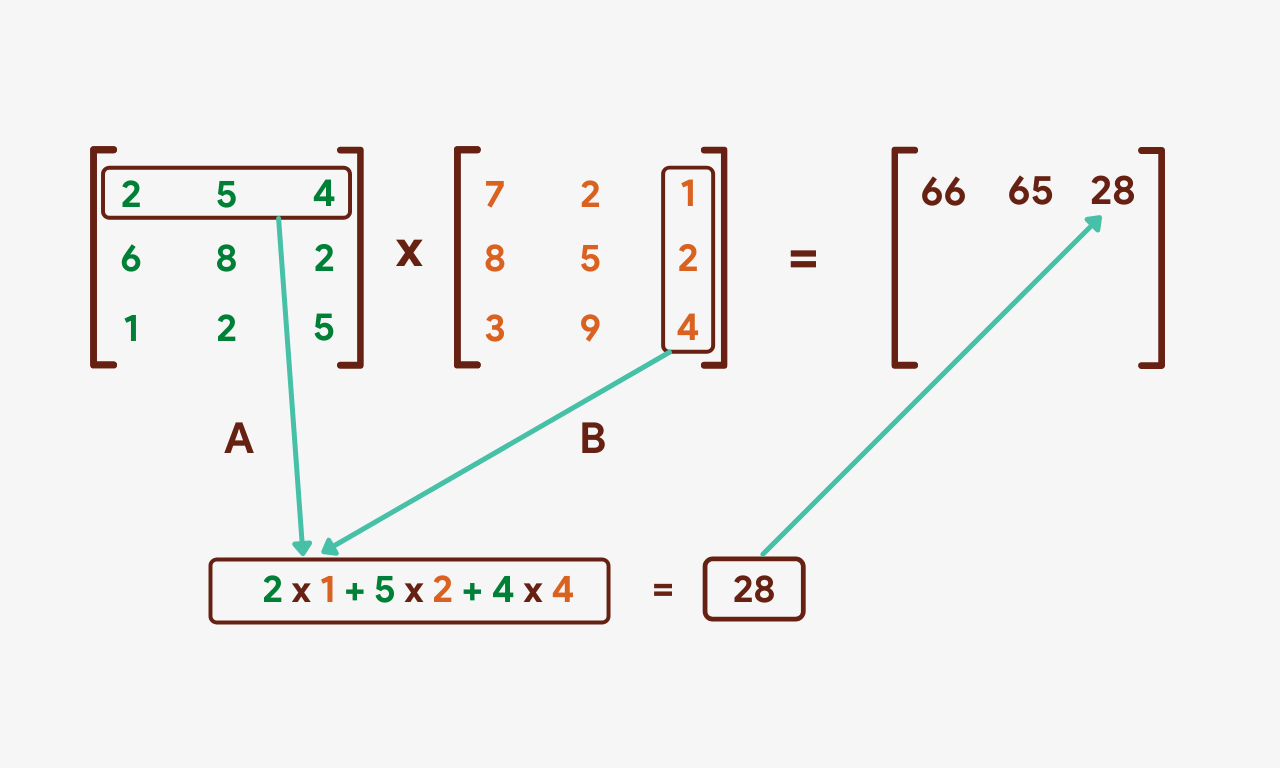
The same process will be repeated for the 3rd column of matrix B.

Allow's repeat this process for the second and 3rd rows of matrix A.

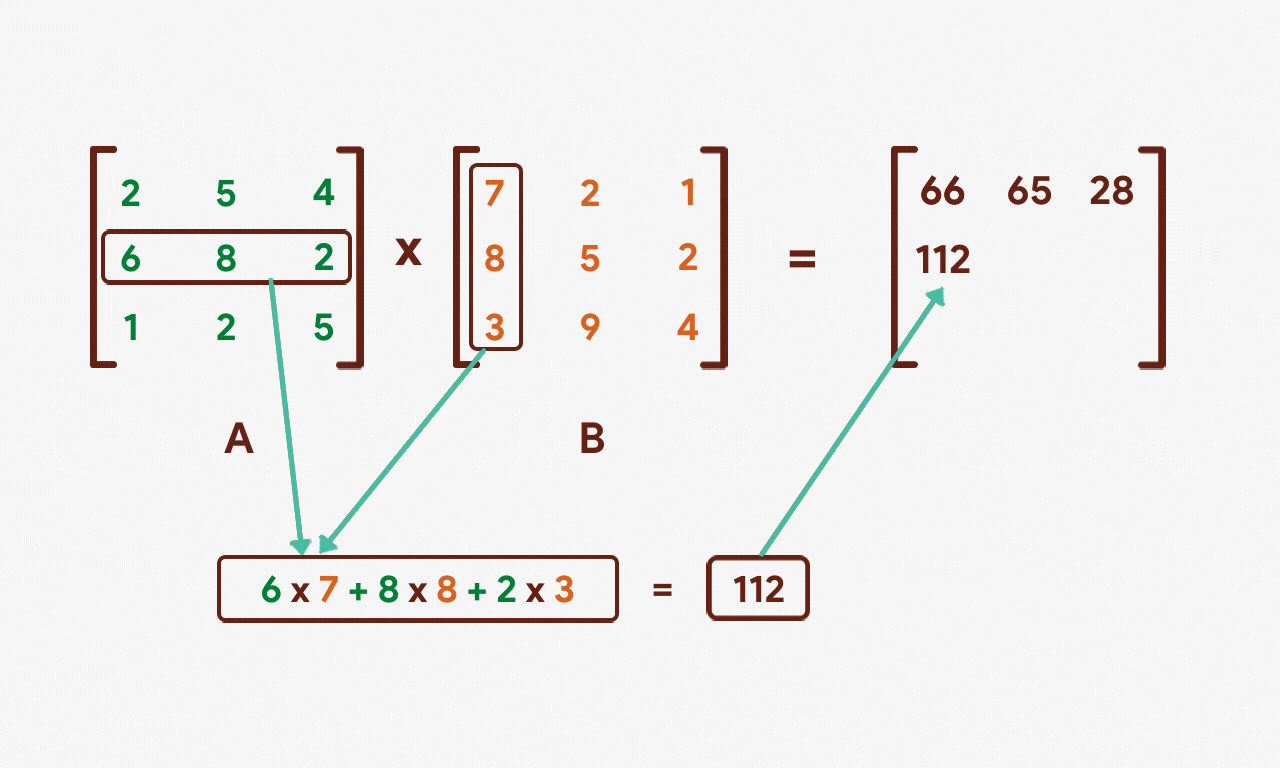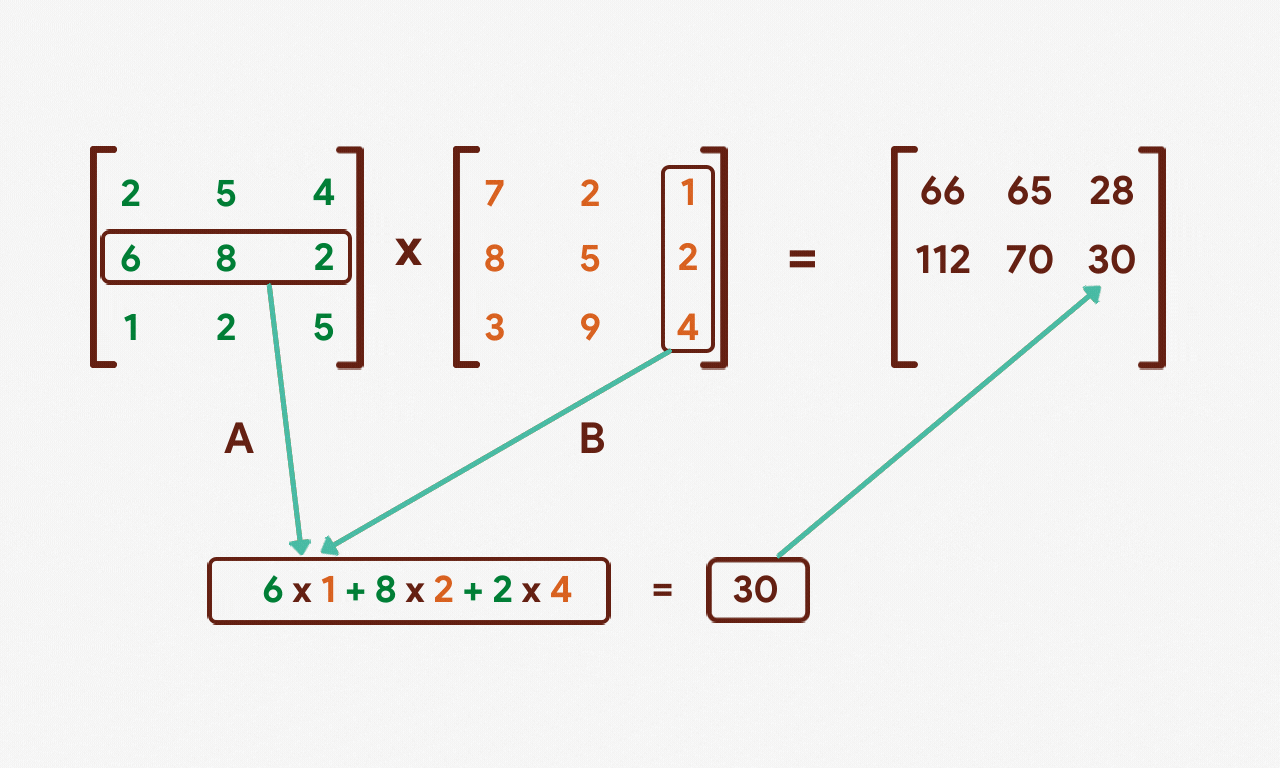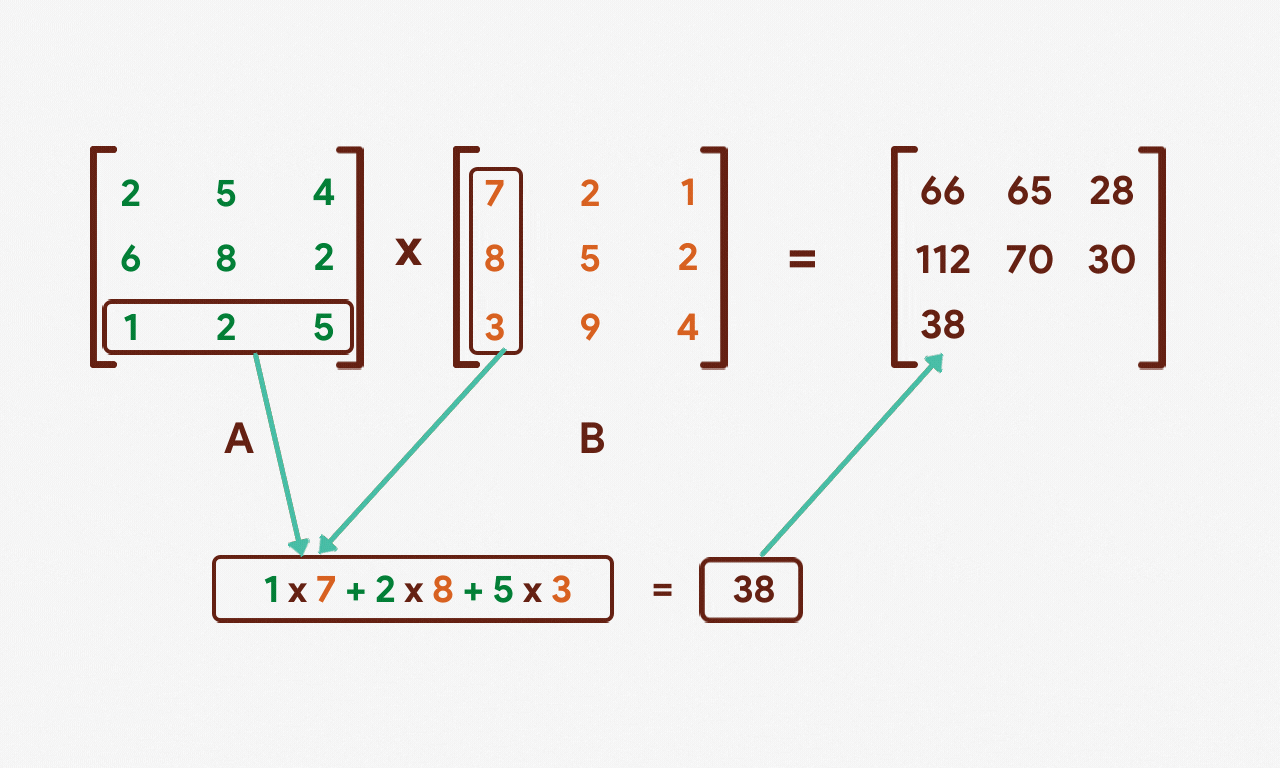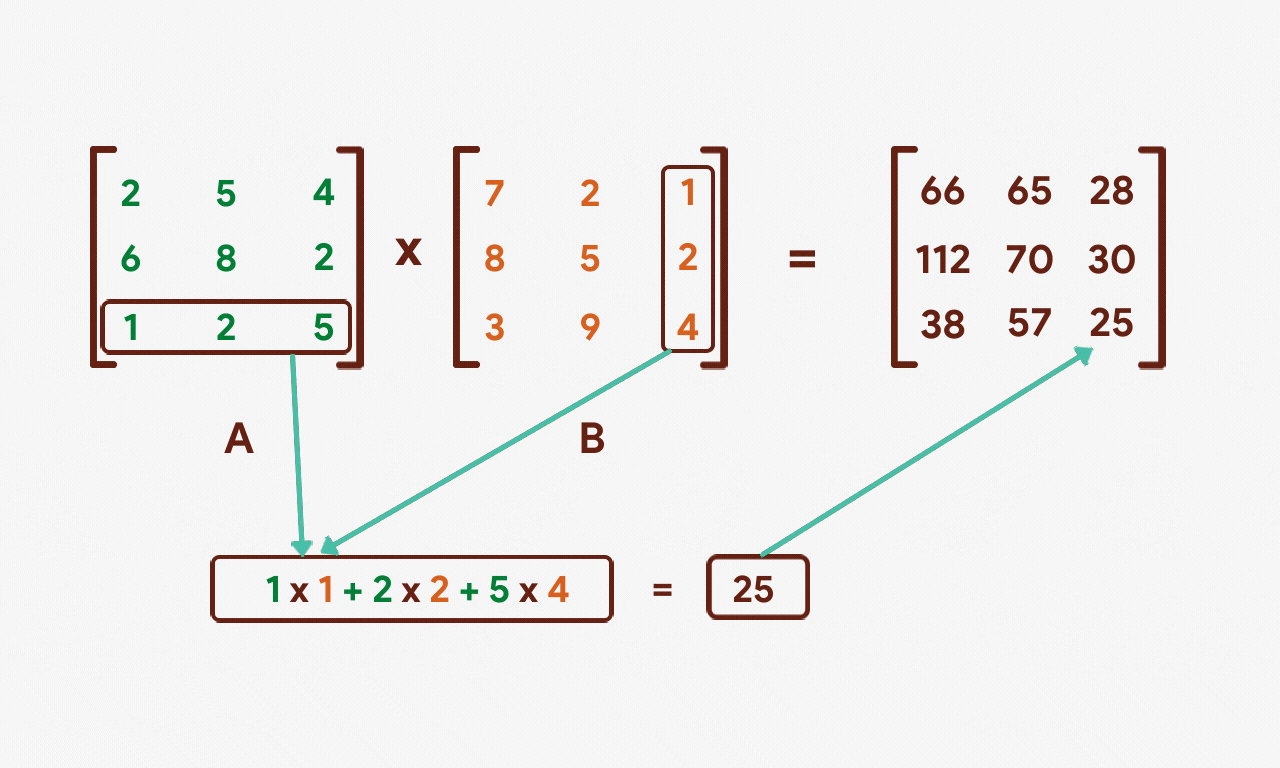
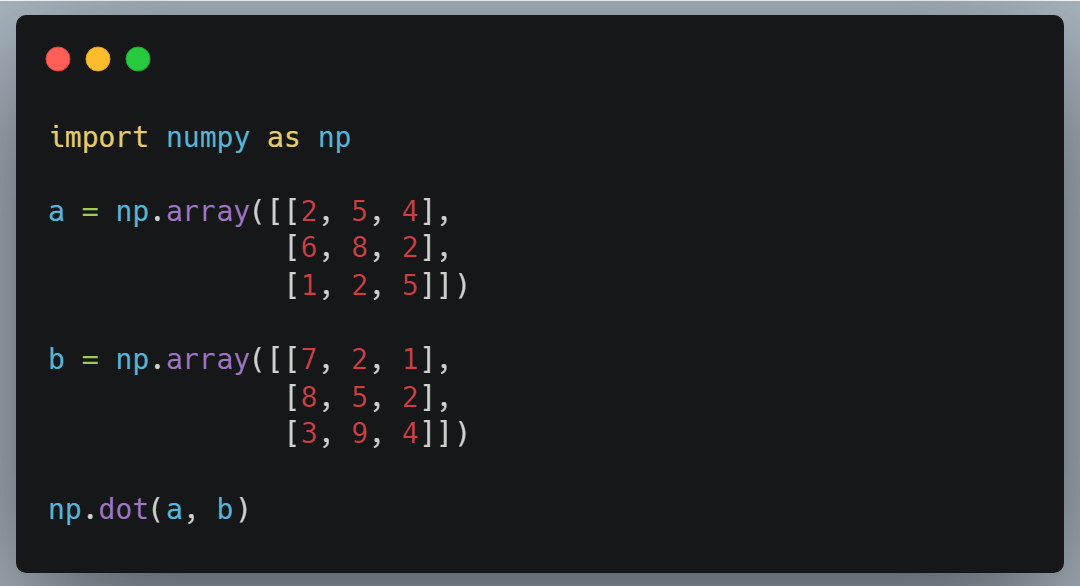
Using NumPy, nosotros can multiply two matrices with each other by using the numpy.dot() function.

There are a few things worth noting about matrix multiplication:

When multiplying two matrices, the number of columns in the get-go matrix must be the same equally the number of rows in the second matrix. In other words, the inner dimensions of the two matrices must be the aforementioned.

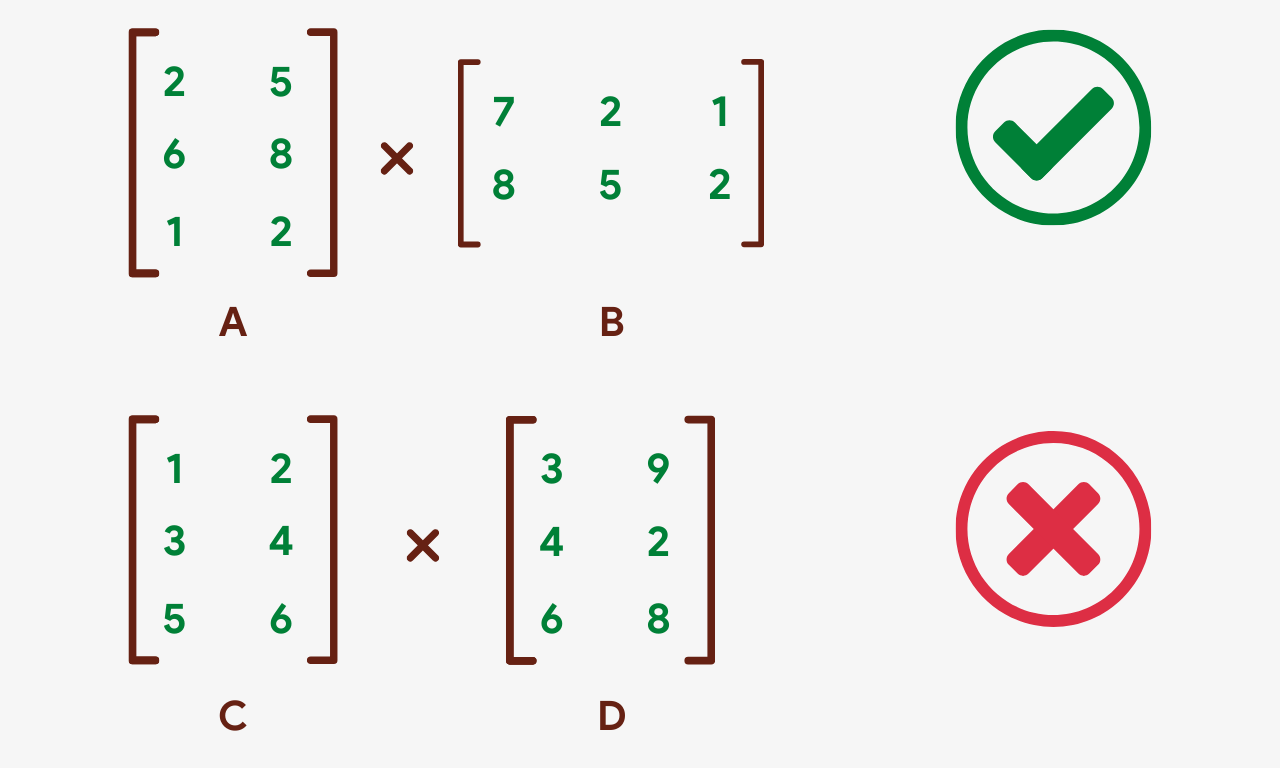
In the in a higher place image, the matrices A and B can be multiplied since A has 2 columns and B has two rows. The matrices C and D tin't be multiplied because C has simply 2 columns while D has 3 rows.

The dimensions of the resulting matrix will exist equal to the outer dimensions of the ii matrices to be multiplied, i.eastward. the resulting matrix will take the number of rows of the first matrix and the number of columns of the second matrix.

The product of ii matrices is NOT commutative. Information technology ways that A multiplied by B is not equal to B multiplied past A.

Transpose of a Matrix

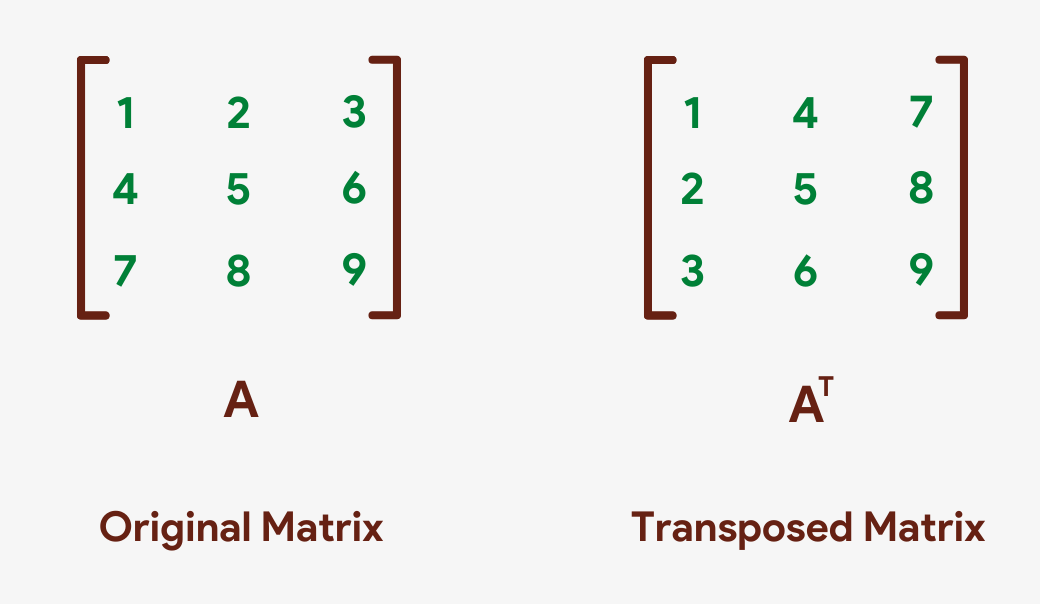
Transposing a matrix means swapping its rows and columns with each other, i.e. changing its rows into columns and columns into rows. The transpose of a matrix is often denoted by a capital letter T in superscript. For example, Aᵀ volition denote the transpose of matrix A.

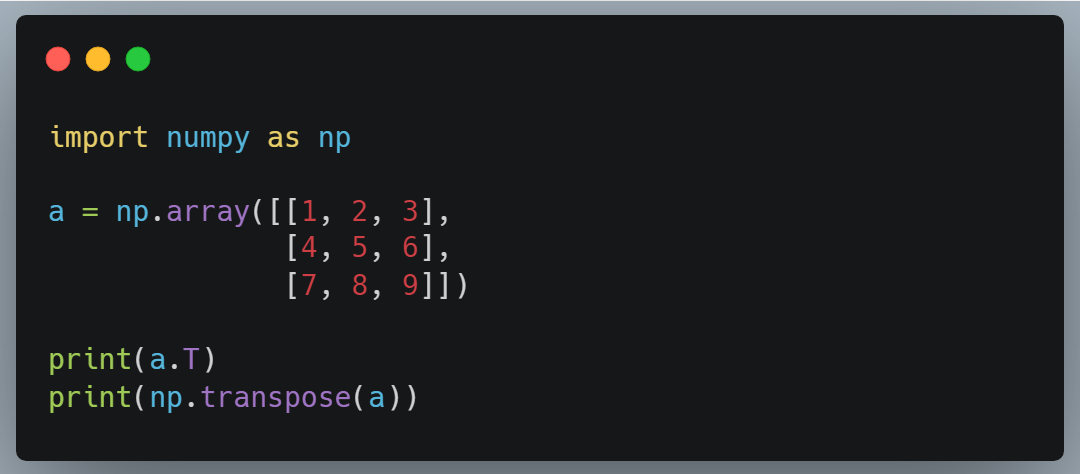
In NumPy, a matrix (array) can be transposed either using the assortment's own .T method or using the numpy.transpose() function.

Vectors

In linear algebra, a vector is a quantity having a direction along with its magnitude. However, this definition is very much Physics-based. Allow's define it in our own terms.

A vector tin can be thought of as an chiliad x 1 matrix or a column matrix. The number of rows in a vector tells the dimension of a vector. For example, a vector having 3 rows will be called a 3-dimensional vector.

Different matrices, vectors are created as 1-d arrays instead of 2-d arrays when using NumPy.

Dot Product of Vectors

When two vectors are multiplied, the issue is a numeric value and is called their dot product.
The dot product of two vectors is calculated by multiplying their respective elements by each other and so summing them all.

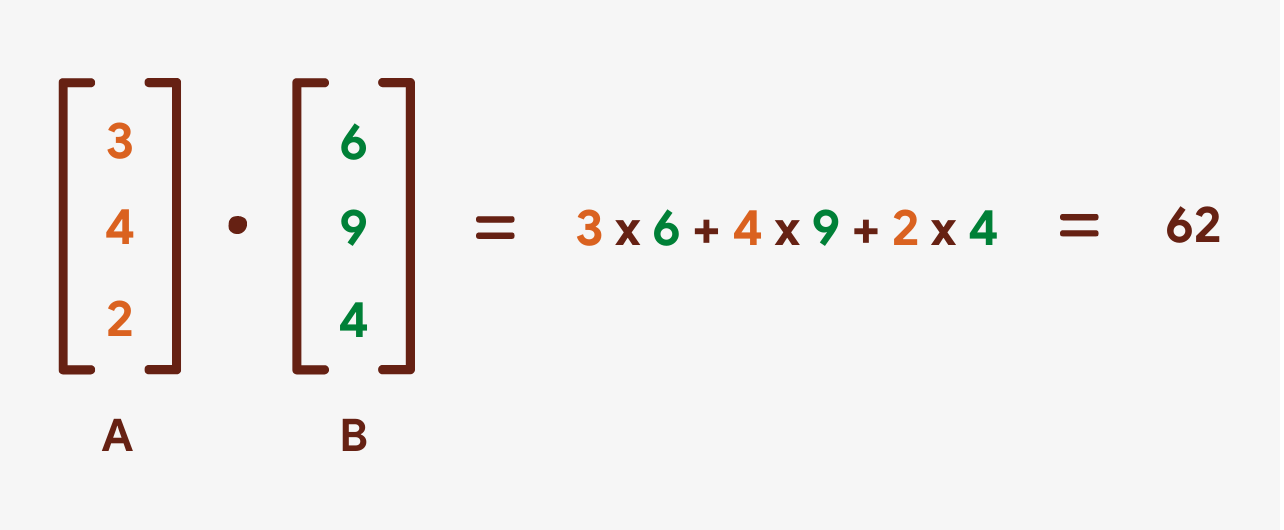
This is how the dot production of two vectors can be calculated using NumPy:

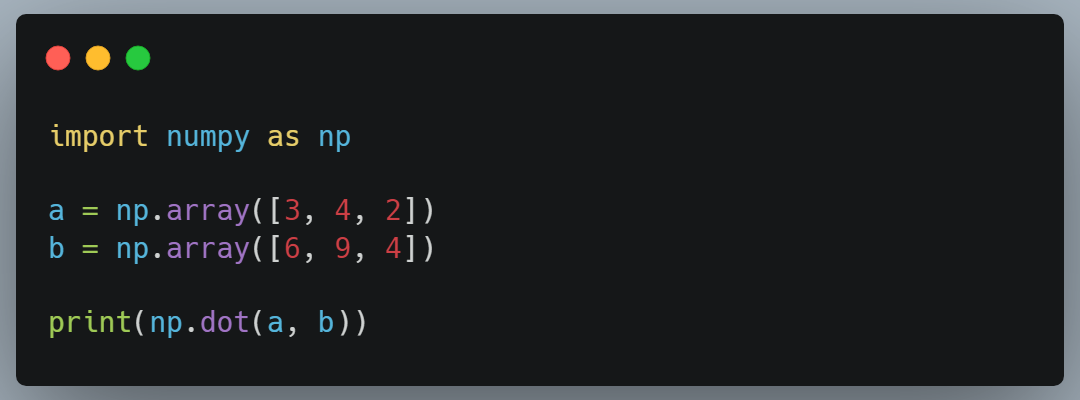
The dimensions of the two vectors should be the same when calculating their dot product.

Unlike matrix multiplication, the dot product of two vectors is commutative, meaning that A • B = B • A.

Conclusion

Using linear algebra makes car learning computation very fast past introducing vectorization. NumPy is i of the libraries used to vectorize machine learning algorithms. This article introduced y'all to some basics of linear algebra for car learning, such as matrices, vectors, matrix addition, multiplication, and the dot product of matrices. The purpose of this guide was to brand you familiar with the basics of linear algebra so that y'all don't feel missed out when looking at the Math backside various auto learning algorithms.